MERCURE, MARS, VENUS, la TERRE : le choc des planètes ( étude de l'Observatoire de Paris )

10 décembre 2012

Est-ce la fin de notre système Solaire ?

Mercure, Mars, Vénus, la Terre:

le choc des planètes!

ARTICLE DEJA PUBLIE LE 12 JUIN 2009 A 14H57

Des collisions planétaires entre Mercure, Mars, Vénus et la Terre sont-elles envisageables ? La question de la stabilité du Système solaire est l'un des plus vieux problèmes de la physique. Pour y répondre, l'équipe de l'Observatoire de Paris menée par Jacques Laskar vient de réaliser une étude statistique inédite sur l'évolution du Système solaire. Dans environ 1 % des cas, les calculs conduisent à des collisions entre planètes ou entre une planète et le Soleil en moins de 5 milliards d'années. Ces résultats sont publiés dans la revue Nature datée du 11 juin 2009.

Le problème de la stabilité du Système solaire a été posé par Isaac Newton après l'énonciation de sa loi de l'attraction universelle. Si l'on considère une planète unique autour du Soleil, on retrouve bien le mouvement elliptique décrit par Kepler. Cependant, dès que plusieurs planètes orbitent autour du Soleil, elles sont soumises à leur attraction mutuelle qui vient perturber leur mouvement. Jusque récemment, les scientifiques ont accepté une image régulière et quasi périodique du mouvement des planètes, ne permettant ni les collisions ni les rencontres proches.

Il y a tout juste 20 ans et grâce aux calculs sur ordinateurs, Jacques Laskar a montré que le mouvement du Système solaire est chaotique. Dès lors, il est devenu impossible de prédire le mouvement des planètes sur une durée de plus de quelques dizaines de millions d'années (Ma). Il n'est plus alors possible de calculer une seule orbite du mouvement pour répondre à la question de la stabilité du Système solaire, c'est à dire décider si la collision d'une planète avec une autre ou avec le Soleil est possible en moins de 5 milliards d'années (Ga), date à laquelle le Soleil parviendra à la fin de sa vie en devenant une géante rouge. En 1994, Jacques Laskar, dans une première étude à long terme, a montré que la diffusion chaotique de l'orbite de Mercure est telle qu'une rencontre proche ou une collision avec Venus est possible en moins de 5 Ga. Pour parvenir à ce résultat, il a utilisé des équations moyennées permettant de diviser par plus de 1.000 les temps de calcul. Cependant, cette approximation n'est plus valable au voisinage de la collision.

Une étude statistique sur un modèle complet, sans moyennisation et incluant les contributions de la relativité générale s'est donc révélée nécessaire. Elle est décrite dans le numéro de Nature du 11 juin 2009. Grâce aux calculs précédemment effectués, il est apparu qu'il fallait réaliser un très grand nombre de simulations du mouvement du Système solaire sur 5 Ga, car l'estimation de la probabilité recherchée est faible. Ainsi, pour obtenir une étude statistique significative, Jacques Laskar et Mickael Gastineau (IMCCE/Observatoire de Paris/UPMC/CNRS) ont calculé plus de 2500 trajectoires d'un modèle réaliste du Système solaire, comprenant la relativité générale et la contribution de la Lune.

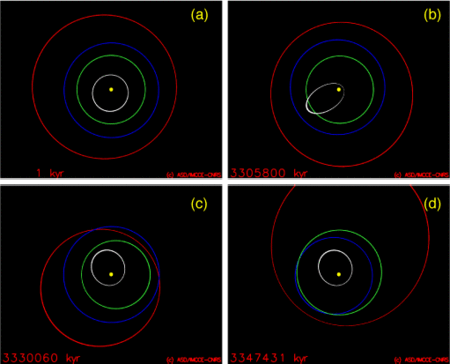
Figure 1: Exemple d'évolution à long terme des orbites des planètes telluriques : Mercure (blanc), Vénus (vert), Terre (bleu), Mars (rouge). Le temps est indiqué en milliers d'années (kyr). (a) Au voisinage de l'état actuel, les orbites se déforment sous l'influence des perturbations planétaires, mais sans permettre de rencontres proches ou de collisions. (b) Dans près de 1% des cas, l'orbite de Mercure peut se déformer suffisamment pour permettre une collision avec Vénus ou le Soleil en moins de 5 Ga. (c) Pour l'une des trajectoires, l'excentricité de Mars augmente suffisamment pour permettre une rencontre proche ou une collision avec la Terre. (d) Ceci entraîne une déstabilisation des planètes telluriques qui permet aussi une collision entre Vénus et la Terre.

Chaque solution nécessitant près de 4 mois de calcul, les chercheurs ont dû faire appel aux ordinateurs de l'Observatoire de Paris, de l'Institut de Physique du Globe, et du noeud EGEE du Laboratoire de l'Accélérateur Linéaire. Finalement, c'est la mise en place de la nouvelle machine JADE du Centre Informatique National de l'Enseignement Supérieur (CINES) qui a permis de trouver les 7 millions d'heures de calcul nécessaires pour mener à bien ce travail. Les 2500 solutions calculées sont compatibles avec notre connaissance actuelle du Système solaire. Dans la majorité des cas, celui-ci continue d'évoluer comme dans les quelques millions d'années actuels : les orbites planétaires se déforment et précessent sous l'influence des perturbations mutuelles des planètes mais sans possibilité de collisions ou d'éjections de planètes hors du Système solaire. Néanmoins, dans 1% des cas environ, l'excentricité de Mercure augmente considérablement. Dans plusieurs cas, cette déformation de l'orbite de Mercure conduit alors à une collision avec Vénus ou avec le Soleil d'ici à 5 Ga, tandis que l'orbite de la Terre reste peu affectée. En revanche, pour l'une de ces orbites, l'augmentation de l'excentricité de Mercure est suivie d'une augmentation de l'excentricité de Mars, et d'une déstabilisation complète du Système solaire interne (Mercure, Vénus, Terre, Mars) dans 3.4 Ga. Sur 201 cas étudiés à partir de cette déstabilisation, 5 finissent par une éjection de Mars hors du Système solaire. Tous les autres conduisent à des collisions entre les planètes ou entre une planète et le Soleil en moins de 100 millions d'années. Un cas aboutit à une collision entre Mercure et la Terre, 29 cas à une collision entre Mars et la Terre et 18 à une collision entre Vénus et la Terre.
La probabilité d'une collision de la Terre avec une autre planète dans les 5 milliards d'années qui suivent est donc inférieure à 1%.

Figure 2: Vue d'artiste d'une collision Vénus-Terre. (J. Vidal-Madjar), (copyright) IMCCE-CNRS.

CNRS press release

Référence

Existence of collisional trajectories of Mercury, Mars and Venus with the Earth
J. Laskar & M. Gastineau
Nature 11/06/2009.

Contact

Jacques Laskar (Observatoire de Paris, IMCCE, et CNRS)